DAG 上的 DP
定义
DAG 即 有向无环图,一些实际问题中的二元关系都可使用 DAG 来建模,从而将这些问题转化为 DAG 上的最长(短)路问题。
解释
以这道题为例子,来分析一下 DAG 建模的过程。
例题 UVa 437 巴比伦塔 The Tower of Babylon
有  种砖块,已知三条边长,每种都有无穷多个。要求选一些立方体摞成一根尽量高的柱子(每个砖块可以自行选择一条边作为高),使得每个砖块的底面长宽分别严格小于它下方砖块的底面长宽,求塔的最大高度。
种砖块,已知三条边长,每种都有无穷多个。要求选一些立方体摞成一根尽量高的柱子(每个砖块可以自行选择一条边作为高),使得每个砖块的底面长宽分别严格小于它下方砖块的底面长宽,求塔的最大高度。
过程
建立 DAG
由于每个砖块的底面长宽分别严格小于它下方砖块的底面长宽,因此不难将这样一种关系作为建图的依据,而本题也就转化为最长路问题。
也就是说如果砖块  能放在砖块
能放在砖块  上,那么
上,那么  和
和  之间存在一条边
之间存在一条边  ,且边权就是砖块
,且边权就是砖块  所选取的高。
所选取的高。
本题的另一个问题在于每个砖块的高有三种选法,怎样建图更合适呢?
不妨将每个砖块拆解为三种堆叠方式,即将一个砖块分解为三个砖块,每一个拆解得到的砖块都选取不同的高。
初始的起点是大地,大地的底面是无穷大的,则大地可达任意砖块,当然我们写程序时不必特意写上无穷大。
假设有两个砖块,三条边分别为  和
和  ,那么整张 DAG 应该如下图所示。
,那么整张 DAG 应该如下图所示。
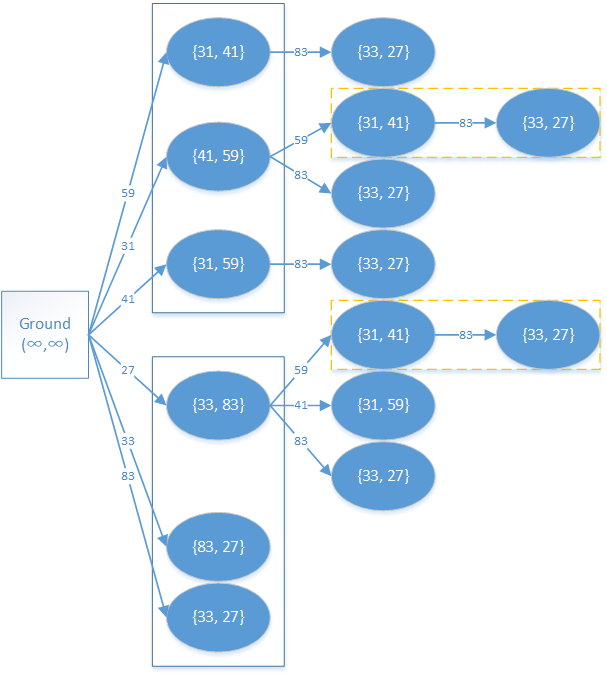
图中蓝色实线框所表示的是一个砖块拆解得到的一组砖块,之所以用  表示底面边长,是因为砖块一旦选取了高,底面边长就是无序的。
表示底面边长,是因为砖块一旦选取了高,底面边长就是无序的。
图中黄色虚线框表示的是重复计算部分,可以采用 记忆化搜索 的方法来避免重复计算。
转移
题目要求的是塔的最大高度,已经转化为最长路问题,其起点上文已指出是大地,那么终点呢?显然终点已经自然确定,那就是某砖块上不能再搭别的砖块的时候。
下面我们开始考虑转移方程。
设  表示第
表示第  块砖块在最下面,且采取第
块砖块在最下面,且采取第  种堆叠方式时的最大高度。那么有如下转移方程:
种堆叠方式时的最大高度。那么有如下转移方程:

其中  是所有那些在砖块
是所有那些在砖块  以
以  方式堆叠时可放上的砖块,
方式堆叠时可放上的砖块, 对应
对应  此时的摆放方式,
此时的摆放方式, 对应砖块
对应砖块  采用第
采用第  种堆叠方式时的高度。
种堆叠方式时的高度。
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69 | #include <cmath>
#include <cstring>
#include <iostream>
using namespace std;
constexpr int MAXN = 30 + 5;
constexpr int MAXV = 500 + 5;
int d[MAXN][3];
int x[MAXN], y[MAXN], z[MAXN];
int babylon_sub(int c, int rot, int n) {
if (d[c][rot] != -1) {
return d[c][rot];
}
d[c][rot] = 0;
int base1, base2;
if (rot == 0) { // 处理三个方向
base1 = x[c];
base2 = y[c];
}
if (rot == 1) {
base1 = y[c];
base2 = z[c];
}
if (rot == 2) {
base1 = x[c];
base2 = z[c];
}
for (int i = 0; i < n; i++) { // 根据不同条件,分别调用不同的递归
if ((x[i] < base1 && y[i] < base2) || (y[i] < base1 && x[i] < base2))
d[c][rot] = max(d[c][rot], babylon_sub(i, 0, n) + z[i]);
if ((y[i] < base1 && z[i] < base2) || (z[i] < base1 && y[i] < base2))
d[c][rot] = max(d[c][rot], babylon_sub(i, 1, n) + x[i]);
if ((x[i] < base1 && z[i] < base2) || (z[i] < base1 && x[i] < base2))
d[c][rot] = max(d[c][rot], babylon_sub(i, 2, n) + y[i]);
}
return d[c][rot];
}
int babylon(int n) {
for (int i = 0; i < n; i++) {
d[i][0] = -1;
d[i][1] = -1;
d[i][2] = -1;
}
int r = 0;
for (int i = 0; i < n; i++) { // 三种建法
r = max(r, babylon_sub(i, 0, n) + z[i]);
r = max(r, babylon_sub(i, 1, n) + x[i]);
r = max(r, babylon_sub(i, 2, n) + y[i]);
}
return r;
}
int main() {
int t = 0;
while (true) { // 死循环求答案
int n;
cin >> n;
if (n == 0) break; // 没有砖头了就停止
t++;
for (int i = 0; i < n; i++) {
cin >> x[i] >> y[i] >> z[i];
}
cout << "Case " << t << ":"
<< " maximum height = " << babylon(n); // 递归
cout << endl;
}
return 0;
}
|
本页面最近更新:2024/7/4 09:48:43,更新历史
发现错误?想一起完善? 在 GitHub 上编辑此页!
本页面贡献者:ouuan, ChungZH, Enter-tainer, iamtwz, Ir1d, isdanni, kenlig, Marcythm, QiuDao2024, sshwy, StudyingFather, Tiphereth-A, TrisolarisHD, ttyS0
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供,附加条款亦可能应用
