跳转至

Stoer–Wagner 算法

定义

由于取消了 源汇点 的定义，我们需要对 割 的概念进行重定义。

（其实是网络流部分有关割的定义与维基百科不符，只是由于一般接触到的割都是「有源汇的最小割问题」，因此这个概念也就约定俗成了。）

割

去掉其中所有边能使一张网络流图不再连通（即分成两个子图）的边集称为图的割。

即：在无向图 中，设 为图 中一些弧的集合，若从 中删去 中的所有弧能使图 不是连通图，称 图 的一个割。

有源汇点的最小割问题

同 最小割 中的定义。

无源汇点的最小割问题

包含的弧的权和最小的割。也称为全局最小割。

显然，直接跑网络流的复杂度是行不通的。

Stoer–Wagner 算法

引入

Stoer–Wagner 算法在 1995 年由Mechthild Stoer与Frank Wagner提出，是一种通过 递归 的方式来解决 无向正权图 上的全局最小割问题的算法。

性质

算法复杂度 一般可近似看作 。

它的实现基于以下基本事实：设图 中有任意两点 。那么任意一个图 的割 ，或者有 在同一连通块中，或者有 是一个 割。

过程

  1. 在图 中任意指定两点 ，并且以这两点作为源汇点求出图 的 最小割（定义为cut of phase），更新当前答案。
  2. 「合并」点 ，如果图 中 大于 ，则回到第一步。
  3. 输出所有cut of phase的最小值。

合并两点 ：删除 之间的连边 ，对于 中任意一点 ，删除 ，并将其边权 加到 上

解释：如果 在同一连通块，对于 中的一点 ，假如 ，那么 也一定成立，否则因为 连通， 连通，导致 在同一连通块，此时 将比 更优。反之亦然。所以 可以看作同一点。

步骤 1 考虑了 不在同一连通块的情形，步骤 2 考虑了剩余的情况。由于每次执行步骤 2 都会使 减小 ，因此算法将在进行 后结束。

S-T 最小割的求法

（显然不是网络流。）

假设进行若干次合并以后，当前图 ，执行步骤 1。

我们构造一个集合 ，初始时令 。

我们每次将 中所有点中，满足 ，且权值函数 最大的节点加入集合 ，直到 。

其中权值函数的定义：

（若 ，则 ）。

容易知道所有点加入 的顺序是固定的，令 表示第 个加入 的点，； 表示 被加入 后 的大小，即 被加入的顺序。

则对任意点 ，一个 到 的割即为 。

证明

定义一个点 被激活，当且仅当 在加入 中时，发现在 此时最后一个点 早于 加入集合，并且在图 中， 与 不在同一连通块。

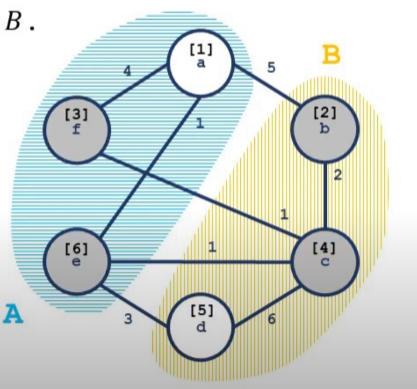
Stoer-Wagner1

如图，蓝色区域和黄色区域为两个不同的连通块，方括号中的数字为加入 的顺序。灰色节点为活跃节点，白色节点则不是活跃节点。

定义 ，也就是严格早于 加入 的点，令 为 的诱导子图（点集为 ）的边集。（注意包含点 。）

定义诱导割 为 。。

Lemma 1

对于任何被激活的点 ，。

证明：使用数学归纳法。

对于第一个被激活的点 ，由定义可知 。

对于之后两个被激活的点 ，假设 ，则有：

又，已知：

并且 联立可得：

由于 对 有贡献而对 没有贡献，在所有边均为正权的情况下，可导出：

由归纳法得证。

由于 ，并且 不在同一连通块，因此 会被激活，由此可以得出 。

P5632【模板】Stoer–Wagner 算法 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <cstring>
#include <iostream>
using namespace std;
constexpr int N = 601;
int fa[N], siz[N], edge[N][N];

int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); }

int dist[N], vis[N], bin[N];
int n, m;

int contract(int &s, int &t) {  // Find s,t
  memset(dist, 0, sizeof(dist));
  memset(vis, false, sizeof(vis));
  int i, j, k, mincut, maxc;
  for (i = 1; i <= n; i++) {
    k = -1;
    maxc = -1;
    for (j = 1; j <= n; j++)
      if (!bin[j] && !vis[j] && dist[j] > maxc) {
        k = j;
        maxc = dist[j];
      }
    if (k == -1) return mincut;
    s = t;
    t = k;
    mincut = maxc;
    vis[k] = true;
    for (j = 1; j <= n; j++)
      if (!bin[j] && !vis[j]) dist[j] += edge[k][j];
  }
  return mincut;
}

constexpr int inf = 0x3f3f3f3f;

int Stoer_Wagner() {
  int mincut, i, j, s, t, ans;
  for (mincut = inf, i = 1; i < n; i++) {
    ans = contract(s, t);
    bin[t] = true;
    if (mincut > ans) mincut = ans;
    if (mincut == 0) return 0;
    for (j = 1; j <= n; j++)
      if (!bin[j]) edge[s][j] = (edge[j][s] += edge[j][t]);
  }
  return mincut;
}

int main() {
  ios::sync_with_stdio(false), cin.tie(nullptr);
  cin >> n >> m;
  if (m < n - 1) {
    cout << 0;
    return 0;
  }
  for (int i = 1; i <= n; ++i) fa[i] = i, siz[i] = 1;
  for (int i = 1, u, v, w; i <= m; ++i) {
    cin >> u >> v >> w;
    int fu = find(u), fv = find(v);
    if (fu != fv) {
      if (siz[fu] > siz[fv]) swap(fu, fv);
      fa[fu] = fv, siz[fv] += siz[fu];
    }
    edge[u][v] += w, edge[v][u] += w;
  }
  int fr = find(1);
  if (siz[fr] != n) {
    cout << 0;
    return 0;
  }
  cout << Stoer_Wagner();
  return 0;
}

复杂度分析与优化

contract操作的复杂度为 。

一共进行 次contract，总复杂度为 。

根据 最短路 的经验，算法瓶颈在于找到权值最大的点。

在一次contract中需要找 次堆顶，并递增地修改 次权值。

斐波那契堆 可以胜任 查找堆顶和 递增修改权值的工作，理论复杂度可以达到 ，但是由于斐波那契堆常数过大，码量高，实际应用价值偏低。

（实际测试中开 O2 还要卡评测波动才能过。）

本页面最近更新：2024/5/2 00:08:23，更新历史
发现错误？想一起完善？ 在 GitHub 上编辑此页！
本页面贡献者：DanJoshua, opsiff, yingqi-z20, aberter0x3f, CroMarmot, Enter-tainer, EntropyIncreaser, iamtwz, ImpleLee, kenlig, Marcythm, Menci, sldpzshdwz, Tiphereth-A, yzy-1
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供，附加条款亦可能应用