可持久化线段树
主席树
主席树全称是可持久化权值线段树,参见 知乎讨论。
关于函数式线段树
函数式线段树 是指使用函数式编程思想的线段树。在函数式编程思想中,将计算机运算视为数学函数,并避免可改变的状态或变量。不难发现,函数式线段树是 完全可持久化 的。
引入
先引入一道题目:给定
你该如何解决?
一种可行的方案是:使用主席树。
主席树的主要思想就是:保存每次插入操作时的历史版本,以便查询区间第
怎么保存呢?简单暴力一点,每次开一棵线段树呗。
那空间还不爆掉?
解释
我们分析一下,发现每次修改操作修改的点的个数是一样的。
(例如下图,修改了
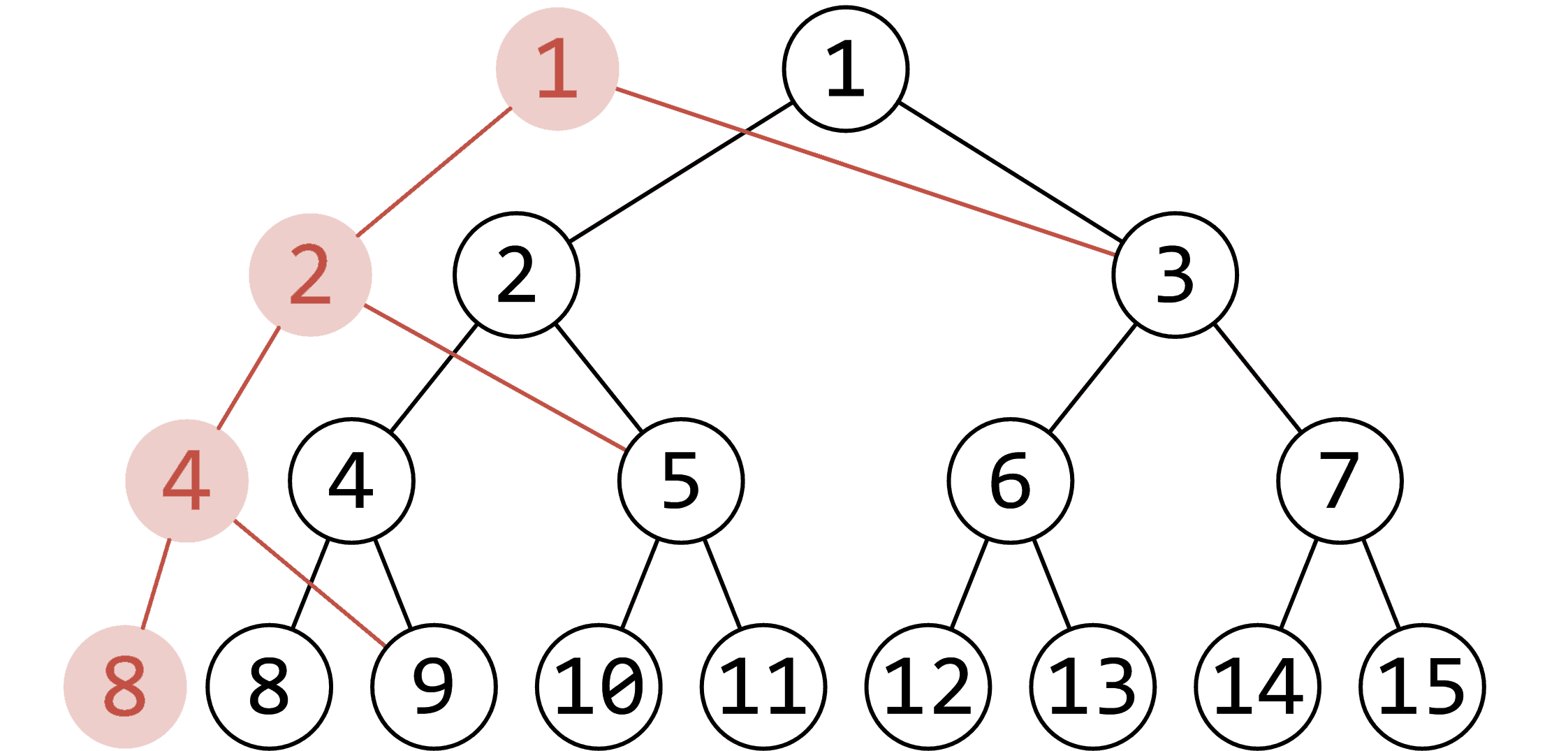
只更改了
注意主席树不能使用堆式存储法,就是说不能用
所以我们只要在记录左右儿子的基础上,保存插入每个数的时候的根节点就可以实现持久化了。
我们把问题简化一下:每次求
怎么做呢?只需要找到插入 r 时的根节点版本,然后用普通权值线段树(有的叫键值线段树/值域线段树)做就行了。
这个相信大家都能理解,回到原问题——求
这里我们再联系另外一个知识:前缀和。
这个小东西巧妙运用了区间减法的性质,通过预处理从而达到
我们可以发现,主席树统计的信息也满足这个性质。
所以……如果需要得到
至此,该问题解决!
关于空间问题,我们分析一下:由于我们是动态开点的,所以一棵线段树只会出现
然后,有
最后给一个忠告:千万不要吝啬空间(大多数题目中空间限制都较为宽松,因此一般不用担心空间超限的问题)!大胆一点,直接上个 n << 5)。
实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 | |
拓展:基于主席树的可持久化并查集
主席树是实现可持久化并查集的便捷方式,在此也提供一个基于主席树的可持久化并查集实现示例。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 | |
参考
https://en.wikipedia.org/wiki/Persistent_data_structure
https://www.cnblogs.com/zinthos/p/3899565.html
本页面最近更新:2024/12/11 21:43:19,更新历史
发现错误?想一起完善? 在 GitHub 上编辑此页!
本页面贡献者:abc1763613206, H-J-Granger, ouuan, Alpha1022, billchenchina, ChungZH, cjsoft, countercurrent-time, EndlessCheng, Enter-tainer, FinParker, Honeta, hsfzLZH1, iamtwz, Ir1d, ksyx, Marcythm, NachtgeistW, renbaoshuo, StudyingFather, SukkaW, Tiphereth-A, william-song-shy
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供,附加条款亦可能应用