数论分块
数论分块可以快速计算一些含有除法向下取整的和式(即形如  的和式)。当可以在
的和式)。当可以在  内计算
内计算  或已经预处理出
或已经预处理出  的前缀和时,数论分块就可以在
的前缀和时,数论分块就可以在  的时间内计算上述和式的值。
的时间内计算上述和式的值。
它主要利用了富比尼定理(Fubini's theorem),将  相同的数打包同时计算。
相同的数打包同时计算。
富比尼定理
又称「算两次」,以意大利数学家圭多·富比尼(Guido Fubini)命名。
富比尼定理的积分形式:只要二重积分  有界,则可以逐次计算二重积分,并且可以交换逐次积分的顺序。
积分号也是特殊的求和号,因此在一般求和中,富比尼定理往往呈现为更换计数顺序,即交换两个求和号。
组合数学中的富比尼定理表现为,用两种不同的方法计算同一个量,从而建立相等关系。
有界,则可以逐次计算二重积分,并且可以交换逐次积分的顺序。
积分号也是特殊的求和号,因此在一般求和中,富比尼定理往往呈现为更换计数顺序,即交换两个求和号。
组合数学中的富比尼定理表现为,用两种不同的方法计算同一个量,从而建立相等关系。
例如这里的双曲线下整点的图片:

图中共分为了  块,这
块,这  块整点的最大纵坐标都相同。如果统计整点的个数,可以从纵向计数改为横向计数,直接计算
块整点的最大纵坐标都相同。如果统计整点的个数,可以从纵向计数改为横向计数,直接计算  个矩形即可。
个矩形即可。
引理 1

略证:

关于证明最后的小方块
QED 是拉丁词组「Quod Erat Demonstrandum」(这就是所要证明的)的缩写,代表证明完毕。现在的 QED 符号通常是  或者
或者  。(维基百科)
。(维基百科)
引理 2

 表示集合
表示集合  的元素个数
的元素个数
略证:
对于  ,
, 有
有  种取值
种取值
对于  ,有
,有  ,也只有
,也只有  种取值
种取值
综上,得证
数论分块结论
对于常数  ,使得式子
,使得式子

成立且满足  的
的  值最大为
值最大为  ,即值
,即值  所在块的右端点为
所在块的右端点为  。
。
证明
令  ,可以知道
,可以知道  。
。
满足条件的所有
过程
数论分块的过程大概如下:考虑和式

那么由于我们可以知道  的值成一个块状分布(就是同样的值都聚集在连续的块中),那么就可以用数论分块加速计算,降低时间复杂度。
的值成一个块状分布(就是同样的值都聚集在连续的块中),那么就可以用数论分块加速计算,降低时间复杂度。
利用上述结论,我们先求出  的 前缀和(记作
的 前缀和(记作  ),然后每次以
),然后每次以 ![[l,r]=[l,\left\lfloor\dfrac n{\lfloor\frac ni\rfloor}\right\rfloor]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7) 为一块,分块求出贡献累加到结果中即可。
为一块,分块求出贡献累加到结果中即可。
伪代码如下:
![\begin{array}{ll}
1 & \text{Calculate $s(i)$, the prefix sum of $f(i)$.} \\
2 & l \gets 1\\
3 & r \gets 0\\
4 & \textit{result} \gets 0 \\
5 & \textbf{while } l \leq n \textbf{ do} : \\
6 & \qquad r \gets \left\lfloor \dfrac{n}{\lfloor n/l \rfloor} \right\rfloor\\
7 & \qquad \textit{result} \gets \textit{result} + [s(r)-s(l-1)] \times\left\lfloor \dfrac{n}{l} \right\rfloor\\
8 & \qquad l \gets r+1\\
9 & \textbf{end while }\\
\end{array}](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
最终得到的  即为所求的和式。
即为所求的和式。
例题:UVa11526 H(n)
题意: 组数据,每组一个整数
组数据,每组一个整数  。对于每组数据,输出
。对于每组数据,输出  。
。
思路
如上推导,对于每一块相同的  一起计算。时间复杂度为
一起计算。时间复杂度为  。
。
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 | #include <iostream>
long long H(int n) {
long long res = 0; // 储存结果
int l = 1, r; // 块左端点与右端点
while (l <= n) {
r = n / (n / l); // 计算当前块的右端点
// 累加这一块的贡献到结果中。乘上 1LL 防止溢出
res += 1LL * (r - l + 1) * (n / l);
l = r + 1; // 左端点移到下一块
}
return res;
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t, n;
std::cin >> t;
while (t--) {
std::cin >> n;
std::cout << H(n) << '\n';
}
return 0;
}
|
向上取整的数论分块
向上取整与前文所述的向下取整十分类似,但略有区别:
对于常数  ,使得式子
,使得式子

成立且满足  的
的  值最大为
值最大为  ,即值
,即值  所在块的右端点为
所在块的右端点为  。
。
注意
当  时,上式会出现分母为
时,上式会出现分母为  的错误,需要特殊处理。
的错误,需要特殊处理。
证明
 ,可以发现
,可以发现  的上取整分块与
的上取整分块与  的下取整分块是一样的。
的下取整分块是一样的。
例题:CF1954E Chain Reaction
题意:有一排  个怪兽,每个怪兽初始血量为
个怪兽,每个怪兽初始血量为  ,一次攻击会使一段连续的存活的怪兽血量减
,一次攻击会使一段连续的存活的怪兽血量减  ,血量不大于
,血量不大于  视作死亡,对于所有
视作死亡,对于所有  求出击杀所有怪兽所需攻击次数,
求出击杀所有怪兽所需攻击次数, 。
。
思路
下面是一种使用二维数论分块的解法:
使用 积木大赛 的技巧,令  ,对于某个
,对于某个  ,答案就是
,答案就是  。
。
对于相邻的两个怪兽,使用二维数论分块,分段求出它们对一段  的答案的贡献,然后差分累加即可。
的答案的贡献,然后差分累加即可。
复杂度  。也存在其他解法。
。也存在其他解法。
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | #include <algorithm>
#include <iostream>
constexpr int N = 100009;
int n, a[N], maxn;
long long ans[N];
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n;
for (int i = 1; i <= n; ++i) {
std::cin >> a[i];
maxn = std::max(maxn, a[i]);
}
for (int i = 0; i < n; ++i)
for (int l = 1, r;; l = r + 1) {
r = std::min(l < a[i] ? (a[i] - 1) / ((a[i] - 1) / l) : N,
l < a[i + 1] ? (a[i + 1] - 1) / ((a[i + 1] - 1) / l)
: N); // 二维数论分块
if (r == N) break;
int x = (a[i + 1] - 1) / l - std::max(a[i] - 1, 0) / l;
if (x > 0) ans[l] += x, ans[r + 1] -= x; // 累加贡献
}
++ans[0]; // ⌈a/l⌉=(a-1)/l+1的式子当a=0时不成立,需要修正
for (int i = 1; i <= maxn; ++i)
std::cout << (ans[i] += ans[i - 1]) << " \n"[i == maxn];
return 0;
}
|
N 维数论分块
求含有  、
、 的和式时,数论分块右端点的表达式从一维的
的和式时,数论分块右端点的表达式从一维的  变为
变为  ,即对于每一个块的右端点取最小(最接近左端点)的那个作为整体的右端点。可以借助下图理解:
,即对于每一个块的右端点取最小(最接近左端点)的那个作为整体的右端点。可以借助下图理解:
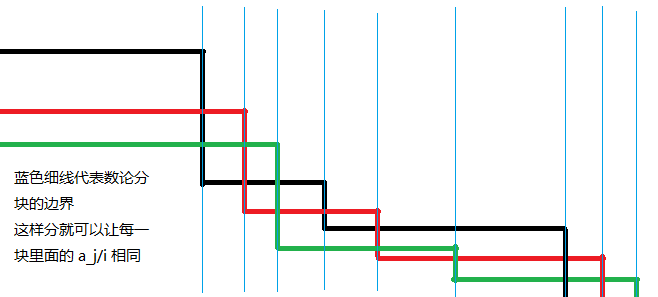
一般我们用的较多的是二维形式,此时可将代码中 r = n / (n / i) 替换成 r = min(n / (n / i), m / (m / i))。
数论分块扩展
以计算含有  的和式为例。考虑对于一个正整数
的和式为例。考虑对于一个正整数  ,如何求出集合
,如何求出集合

的所有值,以及对每一种值求出哪些  会使其取到这个值。可以发现:
会使其取到这个值。可以发现:
- 因为
 是单调不增的,所以对于所有
是单调不增的,所以对于所有  ,使得
,使得  的
的  必然是一段区间。
必然是一段区间。
- 对于任意正整数
 ,我们对
,我们对  与
与  的
的  分别分析,可以发现
分别分析,可以发现  ,取
,取 ![t=\sqrt[3]{n}](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7) 得到
得到  的一个上界为
的一个上界为 ![O(\sqrt[3]n)](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7) 。
。
这些结论与数论分块所需的引理相似,因此猜测可以写为数论分块形式。
结论是:使得式子

成立的最大的  满足
满足  为
为

证明
令  ,那么
,那么

同理  。同时
。同时

又由  以及单调性可推出
以及单调性可推出

所以

进而  是最大的使得
是最大的使得  成立的
成立的  。
。
故原问题可以写为数论分块形式,代码与数论分块形式并无二异。
两个更加通用的结论
对于正整数  和正实数
和正实数  ,我们有
,我们有
- 对于某个不超过
 的正整数
的正整数  ,使式子
,使式子  成立的最大的
成立的最大的  为
为  。
。
- 集合
 的大小不超过
的大小不超过  。
。
习题
-
CQOI2007 余数求和(需要一点转化和特判)
-
UVa11526 H(n)(几乎可以当做模板题)
-
POI2007 ZAP-Queries(数论分块一般配合 莫比乌斯反演 用以进一步降低复杂度;本题需要用到 ![[n=1]=\sum_{d|n}\mu(d)](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7) 这一条莫反结论)
这一条莫反结论)
本页面最近更新:2025/5/24 12:24:08,更新历史
发现错误?想一起完善? 在 GitHub 上编辑此页!
本页面贡献者:2044-space-elevator, 383494, 99-woods, Backl1ght, c-forrest, caijianhong, CCXXXI, ghszt0, Great-designer, iamtwz, ksyx, Marcythm, qwqAutomaton, sshwy, StudyingFather, tder6, Tiphereth-A, TOMWT-qwq, Xeonacid, yusancky
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供,附加条款亦可能应用

